no sistema categorial Graceli, se tem outros parâmetros para energia, massa, momentum, número quântico, e outros.

onde os valores devem ser submetidos ao sistema categorial Graceli.

Matriz categorial de Graceli.

T l    T l     E l       Fl         dfG l   

N l    El                 tf l

P l    Ml                 tfefel 

Ta l   Rl

         Ll

         Dl

Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.

trans-intermecânica de supercondutividade no sistema categorial de Graceli.

EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]

p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.

h e = quantum index and speed of light.

[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..


EPG = GRACELI POTENTIAL STATUS.

[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]

, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].

Propriedades ondulatórias das partículas

Em 1923, o físico francês Louis Victor de Broglie postulou o comportamento ondulatório da matéria:

"Em virtude de os fótons terem características ondulatórias e corpusculares, talvez todas as formas de matéria tenham propriedades ondulatórias e também corpusculares."

Esta foi uma ideia proposta, diferentemente das propostas por Thomson, Rutherford e Bohr, que não tinham evidências experimentais.

Este postulado diz que os elétrons têm também natureza dupla de partícula e onda, sendo acompanhados por uma onda.

Para a frequência f e o comprimento de onda λ da onda, associado ao elétron, ele propôs as equações

   

x

T l    T l     E l       Fl         dfG l   

N l    El                 tf l

P l    Ml                 tfefel 

Ta l   Rl

         Ll

         Dl

onde p é o momento e E a energia do elétron.

Note que a primeira equação é a de Planck, E=hf, para o fóton, agora utilizada para o elétron, e que a equação para λ também vale para

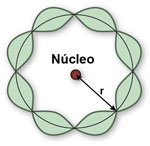
fótons e elétrons. Para os fótons temos que

 x

T l    T l     E l       Fl         dfG l   

N l    El                 tf l

P l    Ml                 tfefel 

Ta l   Rl

         Ll

         Dl

Utilizando a relação entre energia e momento da relatividade especial, E=pc, temos:

x

T l    T l     E l       Fl         dfG l   

N l    El                 tf l

P l    Ml                 tfefel 

Ta l   Rl

         Ll

         Dl

As equações de Louis de Broglie foram propostas para qualquer tipo de matéria. Para corpos macroscópicos, os comprimentos de onda de Broglie são tão pequenos que impossibilitam a sua observação pela interferência ou pela difração. Calcule o comprimento de onda de uma partícula de massa 1g e velocidade 1.000 km/h.

Em 1927, experiências de difração realizadas com elétrons comprovaram as hipóteses de Louis de Broglie.

Função de onda

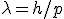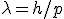Com a comprovação experimental da natureza ondulatória das partículas, e estabelecido o seu comprimento de onda , o próximo passo foi descobrir qual grandeza física está associada à onda de matéria. Nenhuma grandeza física conhecida explica a natureza dessas ondas, então foi utilizada a letra grega Ψ para designar a função de onda da matéria.

Em 1926, Erwin Schrödinger descobriu uma equação que permite encontrar a função de onda de uma partícula, a partir do conhecimento da energia potencial à qual esta está submetida.

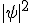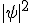Entretanto foi Max Born que, em 1928, descobriu a relação entre a função de onda e a probabilidade de se encontrar a partícula numa determinada posição. Ele concluiu que  é a grandeza estatística que representa a densidade de probabilidade. Esta função dá a probabilidade de encontrarmos uma partícula numa determinada região do espaço.

Com esta última descoberta, a Física Quântica mostra que a natureza possui um comportamento estatístico, sendo descrita por uma função que representa a probabilidade. Este fato incomodou muitos físicos, inclusive Einstein, que expressou sua insatisfação dizendo:

- Deus não joga dados com o Universo.

Entretanto os resultados experimentais dão o veredicto a favor da formulação quântica.

Equação de Schrödinger

  

A Equação de Schrödinger permite calcular a função de onda Ψ (r,t), associada a uma partícula que se move dentro de um campo de forças descrito por um potencial V (r,t). No caso em que o potencial não depende do tempo, ela é expressa do seguinte modo:

x

T l    T l     E l       Fl         dfG l   

N l    El                 tf l

P l    Ml                 tfefel 

Ta l   Rl

         Ll

         Dl

onde  é a constante de Planck normalizada,  o laplaciano e m a massa da partícula.

A resolução da Equação de Schrödinger conduz a um conjunto de funções de onda e a um conjunto de energias correspondentes aos estados do elétron permitidos no átomo. As expressões matemáticas das funções de onda possibilitam determinar a probabilidade de encontrar o elétron na vizinhança de um ponto próximo do núcleo.

No caso do átomo de hidrogênio, a energia potencial eletrostática é dada por

,

x

T l    T l     E l       Fl         dfG l   

N l    El                 tf l

P l    Ml                 tfefel 

Ta l   Rl

         Ll

         Dl

onde e é a carga elementar, ε_o é a constante elétrica de permissividade no vácuo e r é a distância ao centro do átomo. Este é um potencial no espaço tridimensional.

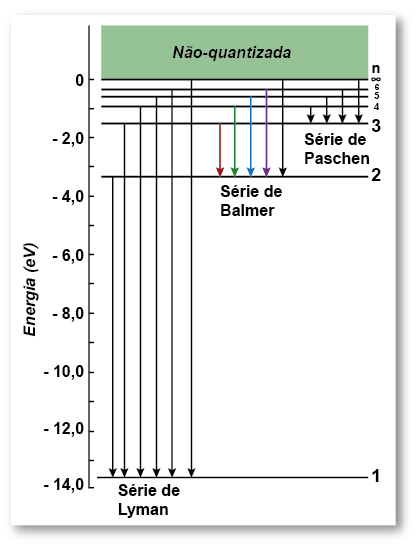
Energias do hidrogênio

A solução da Equação de Schrödinger para este potencial, que não apresentarei aqui, mostra que os valores de energia são quantizados, e são os mesmos obtidos pelo modelo de Bohr.

  

x

T l    T l     E l       Fl         dfG l   

N l    El                 tf l

P l    Ml                 tfefel 

Ta l   Rl

         Ll

         Dl

(Clique na imagem para ampliá-la)

O nível n=1 é o estado fundamental, os outros níveis são estados excitados. O elétron pode receber energia e subir para um desses estados, mas depois de um curto intervalo de tempo volta para o estado fundamental.

Se o elétron estiver no nível fundamental e receber uma energia de pelo menos 13,61 eV, é arrancado do átomo. Temos, neste caso, um elétron livre e um íon do hidrogênio.

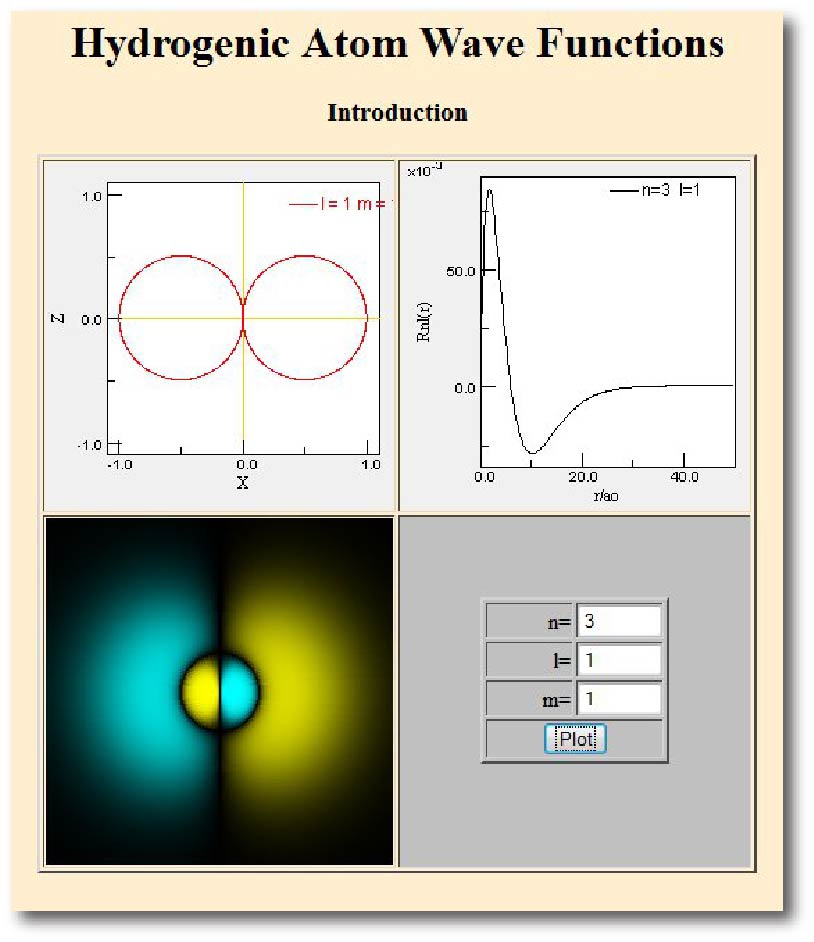
Mais números quânticos

As funções de onda, obtidas a partir da equação de Schrödinger, que descrevem os estados quantizados do átomo de hidrogênio, exigem três números quânticos, correspondentes às três dimensões em que o elétron pode se mover.

Números quânticos do átomo de hidrogênio

Uma função de onda de um estado quântico do átomo de hidrogênio é identificada com um conjunto (n, l, m_l) de números quânticos. O número quântico n determina o nível de energia. O número quântico l é uma medida do módulo do momento angular orbital desse estado quântico. O terceiro número quântico m_l está relacionado à orientação no espaço do vetor momento angular.

Utilize esta simulação (clique na figura) para ver as funções de onda para diferentes valores de (n, l, m_l).